空間分解能・精度で限界を超える高速・立体像再構成手法(RPM法)
従来の画像化レーダ技術は,主に合成開口処理や時間逆伝搬等に基づくため,
特に3次元問題において高分解能イメージングを実現するには,膨大な計算量を要していました.
また,空間分解能は高々波長の半分程度であり,
5 GHz帯域のUWBレーダでも同分解能は約3cm程度となるため,
上記の性能限界が実用化への障壁となっていました.
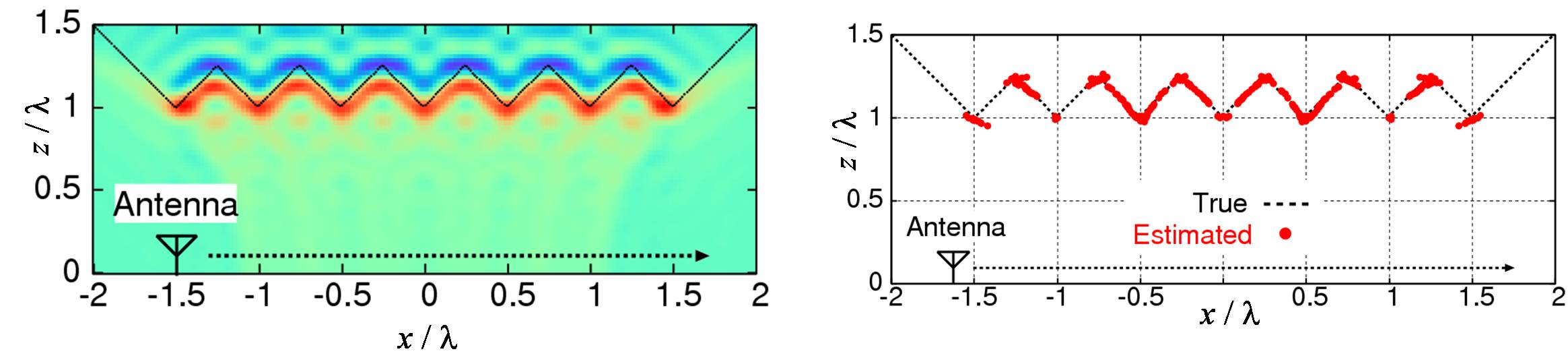
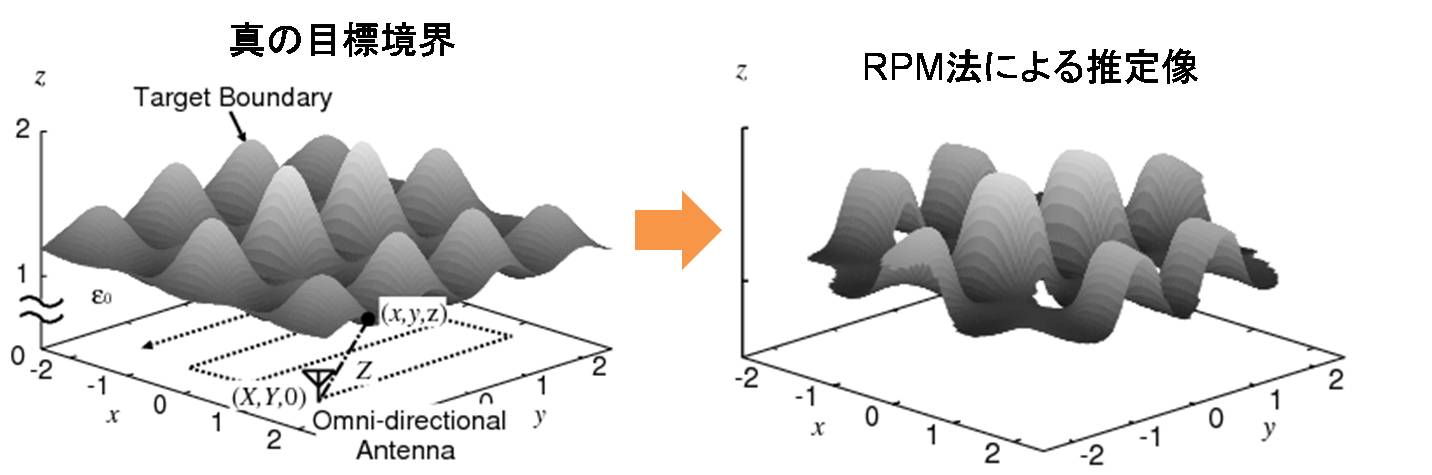
一方,本研究室が独自に開発してきたレーダ技術は,目標境界面抽出に特化することで, 同処理速度を数千倍にも高め,かつUWB信号の超広帯域性を最大限に活用した周波数干渉計法により, 波長限界を超える超分解能(波長の1/10の分解能及び1/100波長の位置決定精度)画像化を実現します. これをRange Points Migration (RPM)法と呼んでいます. 図1は,二次元問題における合成開口処理(SAR)とRPM法の例です. 従来のSARでは,空間分解能が波長により制限されるため,明瞭な境界面が再現されず, 目標の特徴量であるエッジ等が検出されません. これに対し,RPM法では距離情報のみを用いた境界抽出により目標を点群で再現するため, 距離情報が正確に求められれば,超波長分解能の空間分解能を保持します. 図2は,これを3次元問題に拡張した場合であり,この場合も波長よりも小さな規模で 凹凸を有する表面を再現することが可能であることが分かります.
今後の展望
本研究テーマでは,これらの理論を基盤として,観測領域が十分に得られないような状況下や 運動や形状が全く未知の移動目標イメージング等の挑戦的な課題を設定し,世界最先端レベルの研究を実施しています.
[1] Shouhei Kidera, Takuya Sakamoto and Toru Sato,
"Super-Resolution UWB Radar Imaging Algorithm Based on Extended Capon
with Reference Signal Optimization",
IEEE Trans. Antennas & Propagation, vol.59, no. 5, pp.~1606--1615, May, 2011.
[2] Shouhei Kidera, Takuya Sakamoto and Toru Sato,
"Accurate UWB Radar 3-D Imaging Algorithm for Complex
Boundary without Range Points Connections",
IEEE Trans. Geoscience and Remote Sensing,
vol.48, no. 4, pp.~1993--2004, Apr., 2010.
[3] Shouhei Kidera, Takuya Sakamoto and Toru Sato,
"High-resolution and Real-Time 3-D Imaging Algorithm
with Envelope of Spheres for UWB Radars" ,
IEEE Trans. Geoscience and Remote Sensing, vol.46, no.11, pp.3503--3513,
Nov, 2008.
[4] Shouhei Kidera, Takuya Sakamoto and Toru Sato,
"A robust and fast imaging algorithm with an envelope of circles
for UWB pulse radars",
IEICE Trans. Commun., vol.E90-B, no.7, pp. 1801--1809, Jul, 2007.
[5] Shouhei Kidera, Takuya Sakamoto and Toru Sato,
"A high-resolution imaging algorithm without derivatives
based on waveform estimation for UWB pulse radars
IEICE Trans. Commun., vol.E90-B, no.6, pp.1487--1494, Jun, 2007.
一方,本研究室が独自に開発してきたレーダ技術は,目標境界面抽出に特化することで, 同処理速度を数千倍にも高め,かつUWB信号の超広帯域性を最大限に活用した周波数干渉計法により, 波長限界を超える超分解能(波長の1/10の分解能及び1/100波長の位置決定精度)画像化を実現します. これをRange Points Migration (RPM)法と呼んでいます. 図1は,二次元問題における合成開口処理(SAR)とRPM法の例です. 従来のSARでは,空間分解能が波長により制限されるため,明瞭な境界面が再現されず, 目標の特徴量であるエッジ等が検出されません. これに対し,RPM法では距離情報のみを用いた境界抽出により目標を点群で再現するため, 距離情報が正確に求められれば,超波長分解能の空間分解能を保持します. 図2は,これを3次元問題に拡張した場合であり,この場合も波長よりも小さな規模で 凹凸を有する表面を再現することが可能であることが分かります.
今後の展望
本研究テーマでは,これらの理論を基盤として,観測領域が十分に得られないような状況下や 運動や形状が全く未知の移動目標イメージング等の挑戦的な課題を設定し,世界最先端レベルの研究を実施しています.
図1:画像化例(左:SAR,右:RPM)

図2:3次元画像化例(左:真の目標境界,右:RPM法による推定像)

